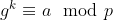
An integer g is a primitive root mod p if every number coprime to p is congruent to a power of g mod p. For every integer coprime to p, there exists an integer k called an index or discrete logarithm of a, such that . Thus, g is a generator of the multiplicative group of integers mod p. The lowest index k of a which is congruent to 1 mod p is the multiplicative order of a mod p. For a to be a primitive root mod p, has to be the smallest power of a for which