You can click on the image to download it in gif format.

You can click on the image to download it in gif format.
Further information on Theory, Apparatus, Procedure, and Helpful Hints is available. Equipment is stored in Rockerfeller Room 402 and 403.
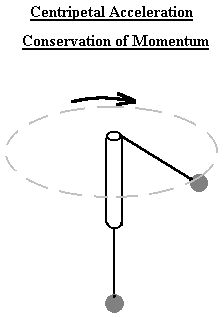
The Centripetal Force Apparatus Kit (PSSC) is used to demonstrate several concepts at once. A hanging mass can provide the force necessary to keep another mass traveling in a circular orbit around the end of a hand-held glass tube. The average human can rotate the glass tube at 2-3 revolutions per second, and exceptional humans moving the tube in tight circles may approach 10 rps. At constant angular velocity, the setup is unstable in the absence of friction, and the friction of a string going over the edge of a glass tube is not highly reproducible, so this is a generally qualitative demonstration.
The simplest of all interesting systems to analyze in terms of rotational kinematics is an orbiting point mass. This mass requires a force to keep it in a circular path, possesses a certain moment of inertia, and has angular momentum. The theoretical treatment can either be in terms of the torque/angular acceleration/MI equations, or in terms of the radial/tangential velocity and acceleration equations, depending on the needs of the course.
The usual use of this demonstration will be to introduce the concept of angular momentum and motion in non-inertial frames, so it is simplest to use the R/Theta formulation. The F=ma equation can be written down as a starting point, and the four terms can be explained with reference to a person moving on a Merry-Go-Round which is (i) at rest, with walking motion along a radius vector, (ii) rotating at a constant angular velocity with the person strapped in a seat, (iii) angular acceleration for a person strapped in a seat, and (iv) a fourth term which it is up to you as the lecturer to explain. (The simplest case I can think of is the description of a model airplane flying in a straight line over the Merry-Go-Round -- the Coriolis term is required to explain why an object with no net force on it appears to fly in a curved path as seen from the rotating frame. However, it is probably easier to talk about angular momentum and show that the Coriolis term is just what is needed to give conservation of angular momentum if there is no net theta force on the body).
If you rotate the mass at the highest angular velocity which you are capable of, the system will be unstable in the absence of friction. There is enough friction in our apparatus to make the demo relatively easy to do, but PRACTICE FIRST! It is probably not worth doing the friction part in quantitative terms -- the most interesting things to see are (i) that the mass can be held at a relatively constant radius, with care, and (ii) that, as you slow your rotation, the rotating mass moves inward and actually increases its linear velocity as work is done on it by the falling of the central mass.
The Centripetal Force Apparatus Kit:
NOTE: The mass is connected to one end of the
string, which runs through the glass tube and connects to the stick
which holds the drilled stopper and a few washers
(1) Don't kill anyone (including yourself) with the swinging stopper and washers.
(2) Friction is significant if you try to pull the hanging mass down and then let it out again to show the slowing (it will slow down too much). It will work to a degree, but after several rotations even the smooth glass rubbing on the string will cause considerable slowdown.