 |
Peter J. ThomasCo-Editor-in-Chief, Biological Cybernetics Professor Office: Yost 212A (216-368-3623) Lab: Yost 212B (216-368-8710) E-mail: pjthomas( AT )case.edu |
| B.A., Yale University, 1990 (Physics and Philosophy) M.S., The University of Chicago, 1994 (Mathematics) M.A., The University of Chicago, 2000 (Conceptual Foundations of Science) Ph.D., The University of Chicago, 2000 (Mathematics) Postdoctoral, The Salk Institute for Biological Studies, 2000-2004 (Computational Neurobiology) |
|
|
Research: Systems & Computational Neuroscience, Theoretical Biophysics, Mathematical Biology, Mathematical Neuroscience, Control & Information Theory in Biology. Simulation and Analysis Codes:
Theses:
Teaching:
Office Hours: (Fall 2023) by appointment. |
|
Pu and Thomas' article ``Fast and Accurate Langevin Simulations of Stochastic Hodgkin-Huxley Dynamics"
provided the cover art for the October 2020 issue of Neural Computation.
Deterministic and stochastic isochrons of a planar conductance based model, see Thomas and Lindner, 2014. Morris-Lecar model with discrete sodium and calcium channels, Anderson et al 2015. Effects of phase offset on response to a two-frequency current stimulus in a cortical cell recorded in vitro. Top: stimulus. Bottom: spike train responses (time vs phase). From Thomas et al 2003. |
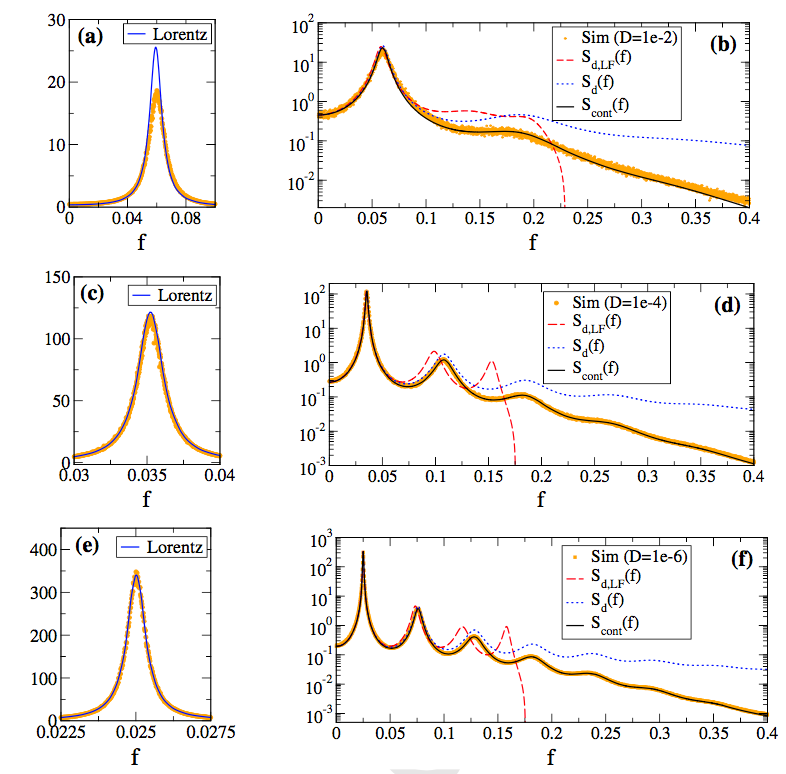
Ion channel fluctuations, irregular synaptic barrages and other sources of ``noise'' limit the precision and reliability with which nerve cells produce action potentials. But highly precise and reliable patterns of spike times have been observed experimentally both in vitro and in vivo. What is the origin and functional significance of precise temporal patterns in the ``neural code''? Problems of current interest include (1) Reexamination of the concept of ``asymptotic phase" and ``asymptotic isostable" coordinates for stochastic oscillators, in collaboration with Prof. Dr. Benjamin Lindner at the Bernstein Center for Computational Neuroscience, Humboldt University, Berlin. (2) Relation of noise spectrum and intensity and input shape and amplitude to spike time precision in single cell models (integrate-and-fire, conductance based models). (3) Data assimilation methods for intracellular recordings of spontaneous spike data in isolated single neurons. (4) Genericity of spike time convergence in simple deterministic neural oscillator models.
|
|
The central nervous system is strongly coupled to the body. Through peripheral receptors and effectors, it is also coupled to the constantly changing outside world. A chief function of the brain is to close the loop between sensory inputs and motor output. It is through the brain's effectiveness as a control mechanism of the body and the external world that it facilitates long-term survival. As part of an ongoing collaboration with the Chiel laboratory, which studies biomechanics and neuromotor control in the marine mollusk Aplysia californica, and the Wilson laboratory, which studies generation and modulation of respiratory rhythms in the mammalian central nervous system, we pursue analysis of feedback control and other mechanisms that endow organisms with robust and flexible rhythm generation.
|
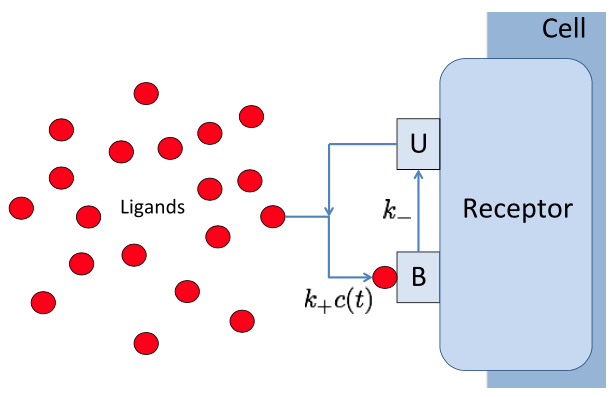
Biochemical signal transduction (two-state BIND channel, Thomas & Eckford (2016) Trans. Info. Thy.). 
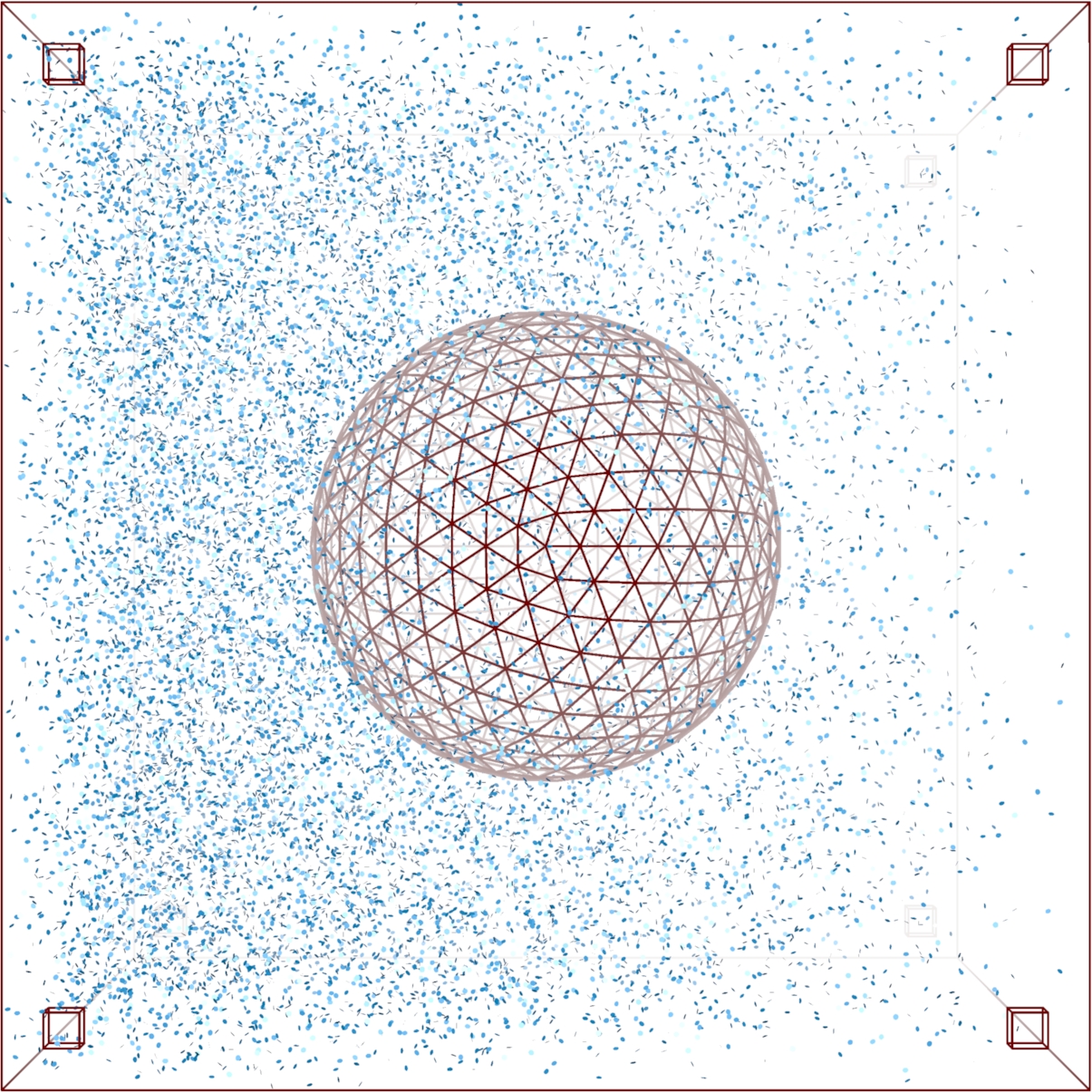
MCell simulation of a cell in a field of signaling molecules. Top: uniform background distribution. Bottom: distribution after imposing flux conditions. |
Signal transduction networks are the biochemical systems by which living cells sense their environments, make and act on decisions -- all without the benefit of a nervous system. How do cells use networks of chemical reactions to process information? In collaboration with Prof. Andrew Eckford of York University, we are combining mathematical ideas from the theory of stochastic point processes and Brownian motion with information theory to develop a framework for understanding information processing in biochemical systems. Projects range from highly theoretical (devising information measures for time varying continuous time Markov processes) to highly computational (simulation of gradient sensing networks using explicit Monte Carlo techniques such as MCell.
|
An Erdos-Renyi network with 50 nodes, connection probability 0.5, and nodes labelled '1' (black) or '0' (gray) with equal probability. Distribution of edge importance measure (Schmidt and Thomas 2014). |
Mathematical models of cellular physiological mechanisms often involve random walks on graphs representing
transitions within networks of functional states.
Schmandt and Galán
recently introduced a novel stochastic shielding approximation as a fast, accurate method for generating approximate
sample paths from a finite state Markov process in which only a subset of states are observable. For example, in ion-channel models,
such as the Hodgkin-Huxley or other conductance-based neural models, a nerve cell
has a population of ion channels whose states comprise the nodes of a graph,
only some of which allow a transmembrane current to pass.
The stochastic shielding approximation consists of neglecting fluctuations in the
dynamics associated with edges in the graph not directly affecting the observable states.
In Schmidt and Thomas 2014 we consider the problem of finding the optimal complexity reducing mapping from a stochastic
process on a graph to an approximate process on a smaller sample space,
as determined by the choice of a particular linear measurement functional on the graph.
The partitioning of ion-channel states into conducting versus nonconducting states provides a case in point.
In addition to establishing that Schmandt and Galánâs approximation is in fact
optimal in a specific sense, we use recent results from random matrix theory
to provide heuristic error estimates for the accuracy of the
stochastic shielding approximation for an ensemble of random graphs.
Moreover, we provide a novel quantitative measure of the contribution of
individual transitions within the reaction graph to the accuracy of the approximate process.
In collaboration with Alan Lerner, director of the Brain Health and Memory Center at CWRU, and Prof. Wojbor Woyczynski we have also applied elementary graph theoretic measures to the analysis of word association networks used as diagnostic tools related to Alzheimer's Disease and other cognitive impairments.
|
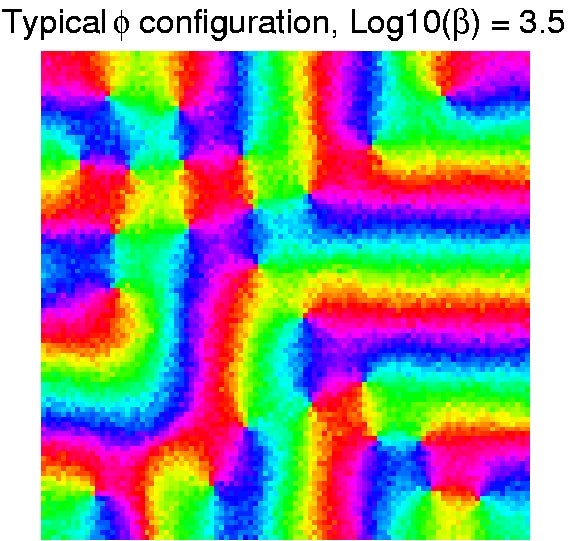
Monte Carlo sampling of the Heisenberg XY Model with (+) center (-) surround lateral interaction. Color represents preferred orientation angle (Thomas 2000, thesis). Bifurcation planform corresponding to a predicted spontaneous hallucination pattern (Bressloff et al 2001A). |
The pathway from the eyes to the visual cortex organizes spontaneously during development using a combination of intrinsic chemical markers and correlation-based, activity-dependent (``Hebbian") mechanisms. The resulting cortical architecture shows fascinating quasiregular patterns with elements including pinwheel and other phase singularity lattices in the cortical maps representing orientation, ocular dominance, retinotopic position and other features of the visual world. Using methods from equivariant bifurcation theory -- the study of branching solutions in the presence of symmetry -- an elegant theory has been developed that accounts for many aspects of the structure of cortical maps. The same mathematical structure underlies the forms of geometric visual hallucinations reported by subjects experiencing sensory deprivation or treatment with mescal, cannabis and other hallucinogens.
|
Anopheles mosquito, capable of transmitting malaria.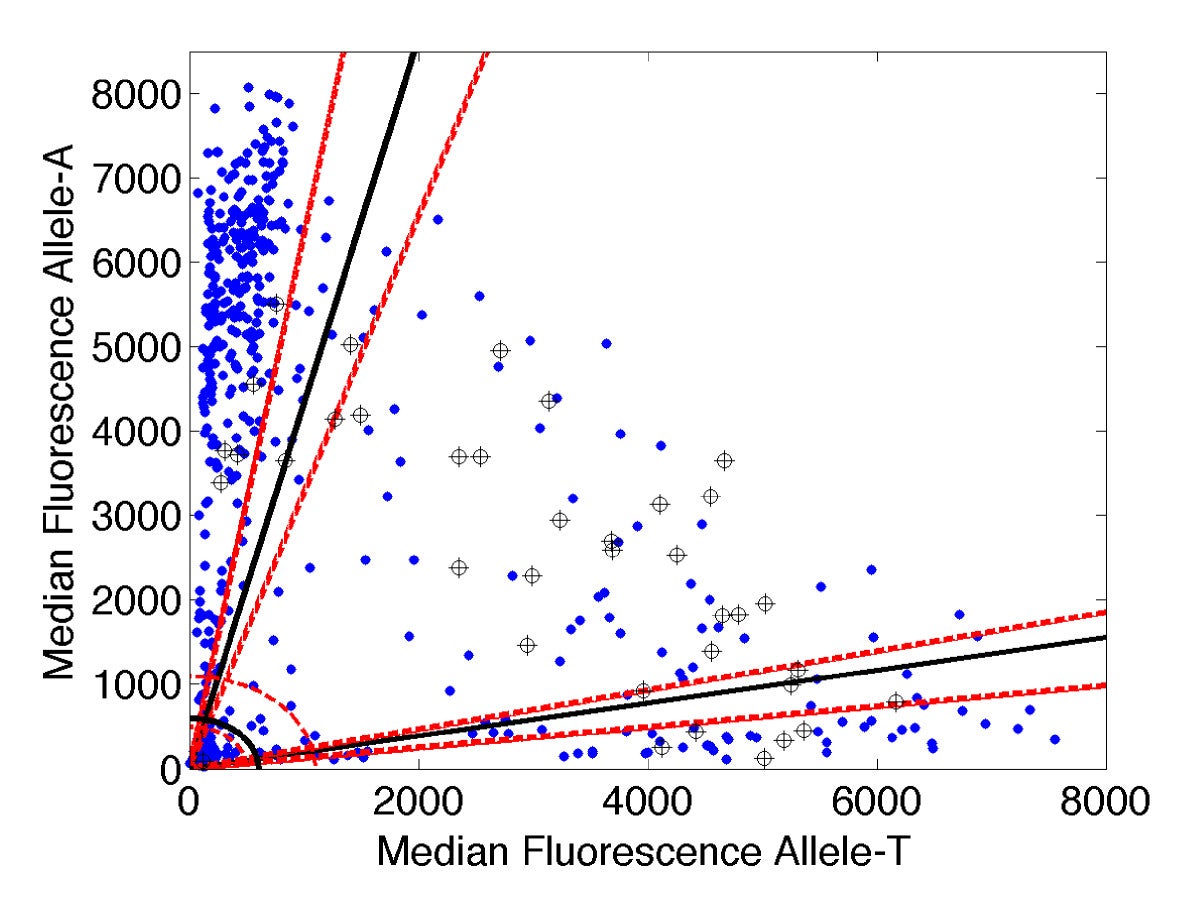 
Analysis of molecular diagnostic data. X-axis: fluorescence signal associated with drug sensitive allele. Y-axis: signal for drug resistant allele. Sloped lines: diagnostic thresholds. |
Molecular diagnostic technology pioneered by collaborator P. Zimmerman in CWRU's Center for Global Health and Diseases promise faster, more accurate means for tracking and combatting the spread of drug resistance in endemic malaria populations worldwide. In order to achieve their potential the new methods require novel analysis tools. Mathematical ideas as simple as coordinate transformation and histogram segmentation have proven effective in boosting the accuracy of molecular genotyping techniques for discriminating drug-sensitive from drug-resistant infections. Recent efforts include development of a method for disambiguating birth and death rates from population time series data, with applications to distinguishing mechanisms of drug resistance.
|
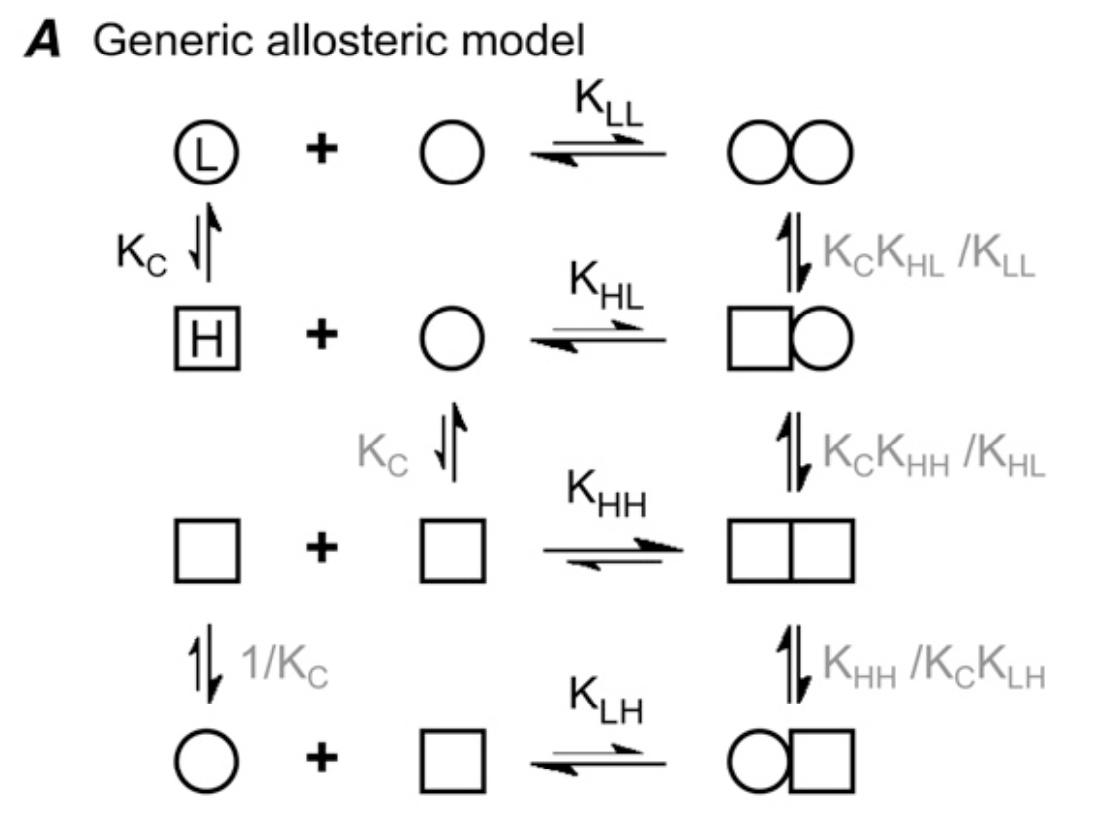Allosteric model for single-stranded polymer formation. From Miraldi et al 2008.
|
Every theorist should have some lab experience.
|
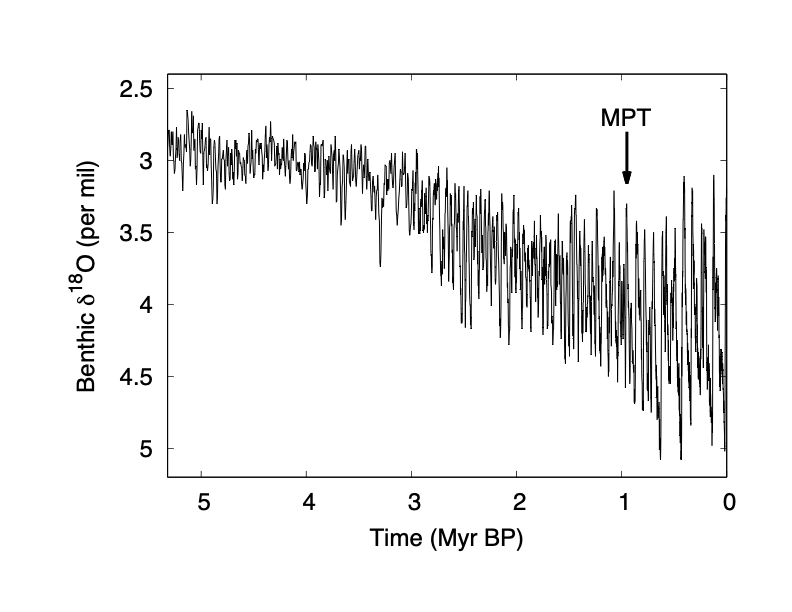Benthic foraminifera $\delta^{18}$O, a proxy for global ice volume and ocean temperature, over the past 3~Myr. From Lisiecki & Raymo, 2005. Redrawn from Omta & Kooi, 2016. Note the change in frequency marked by the arrow.
|
Nonlinear oscillations occur in geological as well as biological systems! In joint work with Earth, Environmental and Planetary Sciences professor Anne Willem Omta we used dynamical systems analysis to evaluate a hypothesis about a possible mechanism for the change in ice-age frequency that occurred roughly one million years ago.
|
Links:
Updated: July 26, 2023
